Det fins mange nettsider og videoer som forklarer hvordan en regulær femkant kan konstrueres ved hjelp av passer og linjal. (Dette er som kjent det klassiske kravet til eksakt konstruksjon.) Istedenfor å lete på nettet etter en oppskrift, vil jeg resonnere meg fram til en måte å konstruere femkanten på. Det er artig å forstå hva man gjør og vite at det er matematisk korrekt. Her er resonnementet.

	Jeg tegnet en regulær tikant. Enheten min er sidekanten, altså 1. Nå har jeg lyst til å regne ut lengden av radius. De ti radiene er like lange, og de ti trekantene er like.
	Her er den ene av de ti trekantene som tikanten består av. Hjørnene kaller jeg A, B og C. Vinkel C er 360/10 = 36 grader. De to andre vinklene må da være 72 grader, siden trekanten er likebeint og vinkelsummen i en trekant er 180 grader.
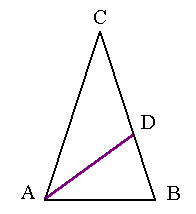	Jeg tegner linja AD slik at den er like lang som AB, altså 1. Siden vinkel B er 72 grader, må vinkel ABD også være 72 grader. Vinkel DAB blir da 180 – 72 – 72 = 36 grader. Og vinkel CAD blir 72 – 36 = 36 grader.
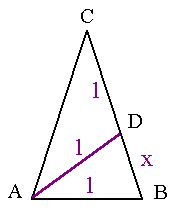	Siden vinkel CAD og vinkel DCA er like store, er trekanten ADC likebeint. Linjene AD og CD må derfor være like lange, det vil si at lengden = 1. Den linjen som vi ikke vet lengden på, er BD, så jeg kaller den for x, og jeg vil regne den ut.
	Trekantene BDA og ABC er likeformete siden de vinklene som tilsvarer hverandre er like store. Derfor kan jeg sette opp en relasjon mellom sidene i de to trekantene.
Jeg kalte lengden av BD for x, og her regner jeg ut den lengden.	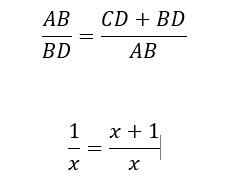Jeg regner ut og får: x ( x + 1) = x x2 + x – 1 = 0
Det vil si: 1x2 + 1x + (-1) = 0 I denne likninga: a =1, b = 1, c = -1	Jeg setter inn i andregradsformelen og regner ut:
Jeg regner ut lengden av BD. Til slutt summerer jeg BD og CD for å finne lengden av BC. Og AB og BC er jo like lange.

Nå kjenner vi lengden av BC og AC, men så er spørsmålet hvordan vi konstruerer den lengden. Det kan Pytagoras hjelpe til med.

	For å vise framgangsmåten, tegner jeg en rettvinklet trekant der de to katetene er 1 og 2 enheter lange. Vi bruker Pytagoras og finner ut at hypotenusen til denne trekanten er kvadratroten av 12 + 22. Det vil si kvadratroten av 5. (Jeg bryr meg ikke om å forklare konstruksjonen av den rettvinklete trekanten.)
	Jeg konstruerer altså den rettvinklete trekanten. Jeg forlenger hypotenusen med 1 enhet, og halverer den linjen jeg får. Nå er de to halvpartene av linjen den lengden som radius skal ha.
	Jeg slår en sirkel med denne lengden som radius, og avsetter enheten ti ganger rundt sirkelens periferi. Her er konstruksjonen. Jeg har også tegnet inn to radier, og forbundet punktene på periferien med hverandre slik at jeg får en regulær femkant og en regulær tikant.

Egentlig kreves det altså to konstruksjoner for å løse oppgaven. Resultatet av den første konstruksjonen er en linje med en lengde som er halvparten av (kvadratroten av 5 + 1). Og den andre konstruksjonen handler om å avsette enheten rundt sirkelperiferien.

Jeg tror at alle korrekte måter å konstruere femkanten på må inkludere den rettvinklete trekanten, men mange oppskrifter slår sammen de to konstruksjonene slik at det er vanskelig å forstå hva som egentlig foregår.

På dette bildet er alle linjene mellom de ti punktene blitt trukket, og jeg har plassert nye mindre femkanter inni hver av de ti likebeinte trekantene som tikanten består av. Under står det fire bilder med varianter av denne ideen, og et bilde som tar ideen videre.